数学物理方法 Mathematic Method in Physics¶

数学物理方法 Mathematic Method in Physics
- Part I : Complex Variable Functions 复变函数

Part I : Complex Variable Functions 复变函数¶

可导与解析¶

复变函数的导数性质¶

$f(z)$可导的必要条件：Cauchy-Reiman Equation

同时对$x$和$y$求偏导：

\[ \begin{aligned} f'(z) = f'(x+iy) &= \frac{\partial f}{\partial x} = \frac{\partial u}{\partial x} + i\frac{\partial v}{\partial x}\\ &= \frac 1i \frac{\partial f}{\partial y} = -i\frac{\partial u}{\partial y} + \frac{\partial v}{\partial y} \end{aligned} \]

即有

\[ \boxed{ \begin{cases} \displaystyle{\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}} \\ \displaystyle{\frac{\partial u}{\partial y} =-\frac{\partial v}{\partial x}} \end{cases} } \]

解析：复变函数在某一区域内可导，而不能是在某一点或某一线上可导。

Cauchy-Reiman Equation

计算$|z|$是否可导/解析？

$|z| = \sqrt{x^2+y^2}$，所以$u=\sqrt{x^2+y^2}$，$v = 0$，计算偏导数得到：

\[ \begin{gathered} \frac{\partial u}{\partial x} = \frac{x}{\sqrt{x^2+y^2}}, \frac{\partial u}{\partial y} = \frac{y}{\sqrt{x^2+y^2}}, \quad \frac{\partial v}{\partial x} = \frac{\partial v}{\partial y} = 0 \end{gathered} \]

可见$\begin{cases} \displaystyle{\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}} \\ \displaystyle{\frac{\partial u}{\partial y} =-\frac{\partial v}{\partial x}} \end{cases}$不能同时满足，故不解析。

计算$u(x,y)$的二阶微分有：

\[ \begin{aligned} \nabla^2u &= \frac{\partial^2u}{\partial x^2}+ \frac{\partial^2u}{\partial y^2}\\ &= \frac{\partial}{\partial x}\frac{\partial v}{\partial y} + \frac{\partial}{\partial y}(-\frac{\partial v}{\partial x})\\ &=0 \end{aligned} \]

同理有：

\[ \nabla^2v = 0 \]

这被称为 (共轭)调和函数 ，其充分条件是满足Cauchy-Reiman方程。

同理还可证：

\[ \nabla^2(uv) =0 \]

Note

很多情况下$u(x,y)$和$v(x,y)$均为初等函数，根据二阶导有：

\[ \frac{\partial^2u}{\partial x^2} = \frac{\partial^2u}{\partial y^2} = \frac{\partial^2u}{\partial (xy)} = 0 \]

通过积分求解解析函数¶

我们知道

\[ dv = \frac{\partial v}{\partial x}dx + \frac{\partial v}{\partial y}dy = -\frac{\partial u}{\partial y}dx + \frac{\partial u}{\partial x}dy \]

因此，只要知道任一解析函数的实部$u(x,y)$或虚部$v(x,y)$，即可求出其另外一个部分

Eg1

$f(z)$解析且$\mathrm{Re} f = u(x,y) = 2xy$, 求$f(z)$

观察有$dv = -2xdx + 2ydy = d(y^2-x^2)$，于是$v = y^2-x^2+C$

\[ f(z) = 2xy + i(y^2-x^2+C) = -i(x+iy)^2 + iC = -iz^2+iC \]

采取共轭复数的求解（不积分）¶

\[ \begin{cases} x= \displaystyle{\frac{z+z^*}{2}}\\ y= \displaystyle{\frac{z-z^*}{2i}} \end{cases} \]

于是

\[ \frac{\partial f}{\partial z^*} = \frac{\partial f}{\partial x}\frac{\partial x}{\partial z^*} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial z^*} = \frac 12 \frac{\partial f}{\partial x} - \frac{1}{2i}\frac{\partial f}{\partial y} = 0 \]

这意味着$f$与$z^*$无关。又有

\[ \begin{aligned} f(x+iy) &= u(x,y)+iv(x,y)\\ f^*(x-iy) &= u(x,y)-iv(x,y) \end{aligned} \]

若已知实部，我们有：

\[ u(x,y) = \frac{f(x+iy)+f^*(x-iy)}{2} \]

若令：$x+iy = z, x-iy = 0$，则$x=\frac z2,y = \frac{z}{2i}$

\[ \begin{aligned} f(z) &= 2u(\frac z2,\frac{z}{2i}) -f^*(0) \\ &= 2u(\frac z2,\frac{z}{2i}) - u(0,0) + iv(0,0)\\ &= 2u(\frac z2,\frac{z}{2i}) - u(0,0) + iC \end{aligned} \]

Note

若函数在0处无定义，可取解析域内$x-iy = z_0$。eg：$u = \frac{x}{x^2+y^2}$

Warning

此处的$z$和$z^*$为“形式化推导”的产物，即两者并不存在数量关系（不一定同时等于0）

特殊情况下的处理¶

Eg2

$f(z)$解析且已知$u+v$，求$f(z) = u+iv$

设

\[ F = u+v+\mathrm{Im}(F) = u+v + iv-iu = (1-i)f \]

此时退化成$U(x,y) = u+v$已知的解析函数求解。

Eg3

$f(z)$解析且已知$uv$，求$f(z) = u+iv$

求平方有：

\[ f^2 = u^2 - v^2 + i(2uv) = U(x,y) + iV(x,y) \]

此时退化成$V(x,y) = 2uv$已知的解析函数求解。

初等函数¶

幂函数¶

\[ f(z) = z^n,\quad n\in\mathbb{C} \]

for $n = 1,2,3 ...$,$f(z)$在$\infty$不解析，但在$\mathbb{C}$解析

for $n = -1,-2,-3 ...$, $f(z)$在$\mathbb{C}/0$上解析

指数函数¶

\[ f(z) = e^z \]

表现为周期函数且$e^x>0\quad if\quad x\in\mathbb{R}$

$e^z+1=0$在$\mathbb{R}$内无解但在$\mathbb{C}$内有无穷多解，since $e^{i\pi + 2k\pi} = -1$

于是其解$z = i\pi + 2k\pi$

实部图像	虚部图像

undefined

三角函数¶

\[ f(z) = \sin z, \cos z, \tan z, \cot z \]

对于复数域可能有$|\sin z| > 1$

由欧拉公式我们有：

\[ \begin{aligned} \sin z &= \frac{e^{iz} - e^{-iz}}{2i} \\ \cos z &= \frac{e^{iz} + e^{-iz}}{2} \end{aligned} \]

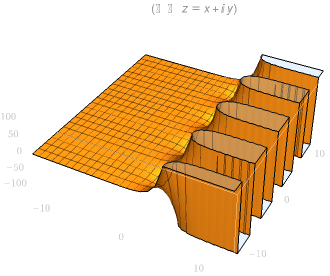
sin(z)实部图像	sin(z)虚部图像

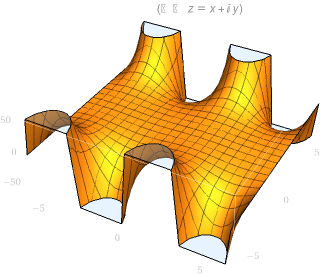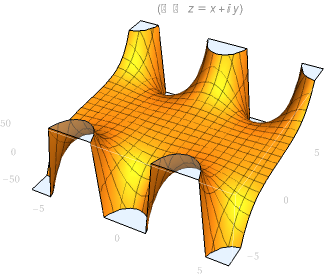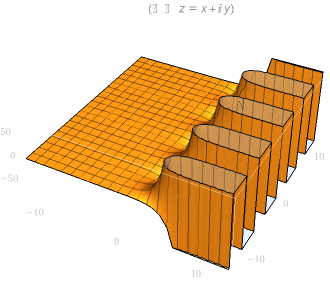
cos(z)实部图像	cos(z)虚部图像

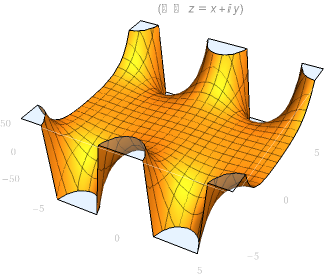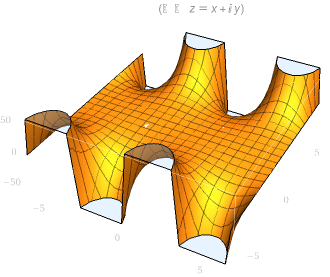双曲函数形式：

\[ \begin{aligned} \sinh z &= \frac{e^z - e^{-z}}{2} \\ \cosh z &= \frac{e^z + e^{-z}}{2} \end{aligned} \]

若要讨论函数在无穷远点的性质，取变量替换$t = \frac 1z$

本性奇点：既非极点，也不可去。eg：

\[ e^{1/z} \quad \text{for} \quad z=0 \]

Essential_singularity

多值函数¶

根式函数的多值性¶

讨论函数：

\[ \begin{aligned} w &= \sqrt{z-a}\\ w^2 &= z-a \end{aligned} \]

若令$w = \rho e^{i\phi}$, $z-a = r e^{i\theta}$

\[ \rho^2 e^{i2\phi} = re^{i\theta} \]

于是

\[ \begin{cases} r = \sqrt{\rho}\\ \theta = 2\phi + 2k\pi \end{cases} \]

即为$\mathrm{arg}(\sqrt{z-a}) = \frac 12 \mathrm{arg}(z-a)$，这意味着对于函数$w$，如果考虑$z$在$a$点附近旋转一圈，在$w$平面上只旋转了半圈。

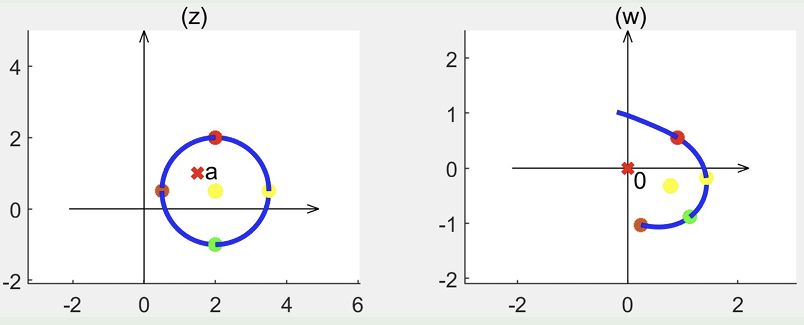
multivalued

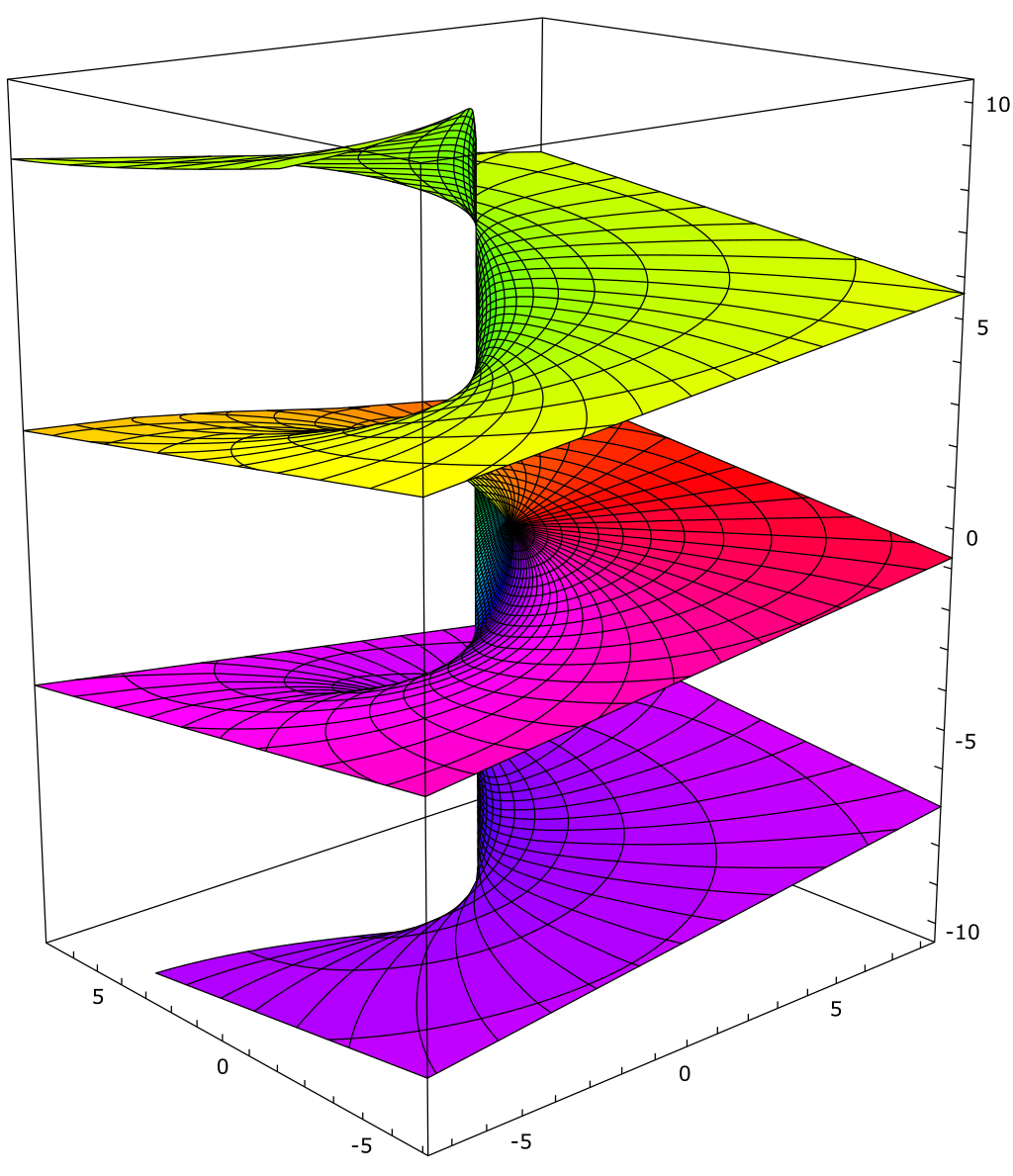
$\sqrt{z}$的图像如下图所示，可见虚部是螺旋上升的：

实部图像	虚部图像

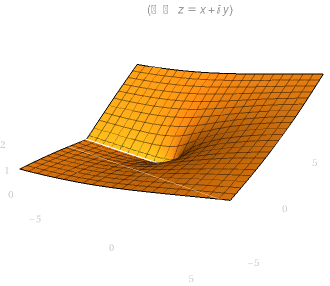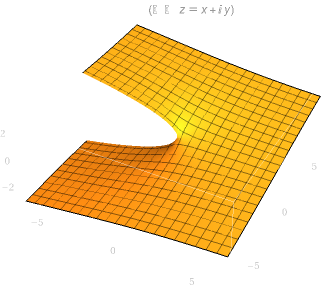这种单一自变量对应多个函数值的函数被称为多值函数

多值函数的单值化¶

考虑模和辐角：

\[ \begin{gathered} |w| = \sqrt{|z-a|} \\ \arg{w} = \frac 12\arg(z-a) \end{gathered} \]

可见其多值性体现在辐角而不是模上（相差$\pi$而不是$2\pi$）

\[ \frac 12 (\arg(z-a)+2\pi) = \arg w+\pi \]

多值性的根源：宗量（作为自变量的函数）$z-a$具有任意性

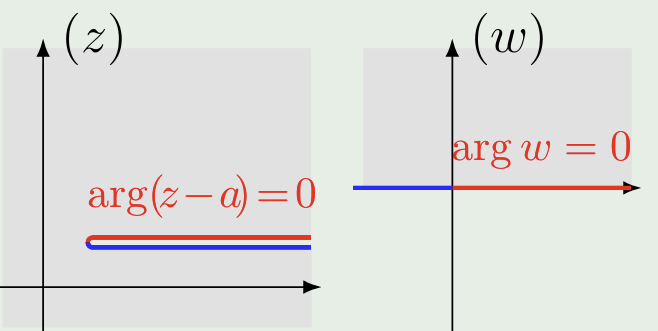
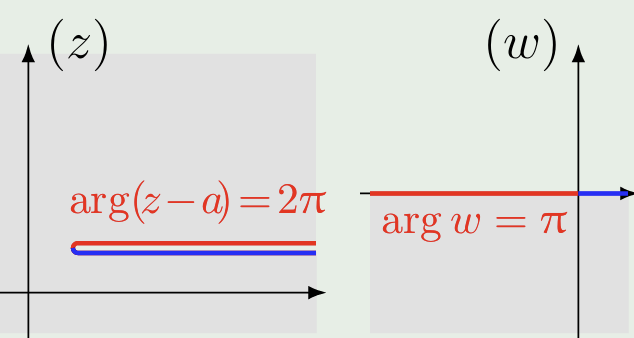
简单的办法是限制其辐角变化范围（$\arg(z-a) \in [0,2\pi)$），即在平面上作割线，此时$\arg w \in [0,\pi)$，意味着$w$只位于平面上半部分，这被称为一个单值分支

此处割线的作用是限制辐角的变化方式，规定割线上岸为$\arg(z-a)=0$

同理，如果限制$\arg(z-a) \in [2\pi, 4\pi)$，有$\arg w \in [\pi,2\pi)$，这是$\sqrt{z-a}$的另一个单值分支：

单值分支I	单值分支II

据此可以判断这一类函数的多值性。

判断函数的多值性

判断以下函数是否为多值函数

\[ (1)\sin \sqrt{x}, (2)\cos \sqrt{x}, (3)\frac{\sin \sqrt{x}}{\sqrt {x}}, (4)\frac{\cos \sqrt{x}}{\sqrt {x}} \]

由根式函数的两个分支互为相反数，可注意到：

\[ \cos (-w) = \cos(w), \frac{\sin (-w)}{-w} = \frac{\sin (w)}{w} \]

即(2)(3)中两个分支中，每一对相反数函数值均相同，可视为一个单值分支。于是(2)(3)为单值函数。

分支点¶

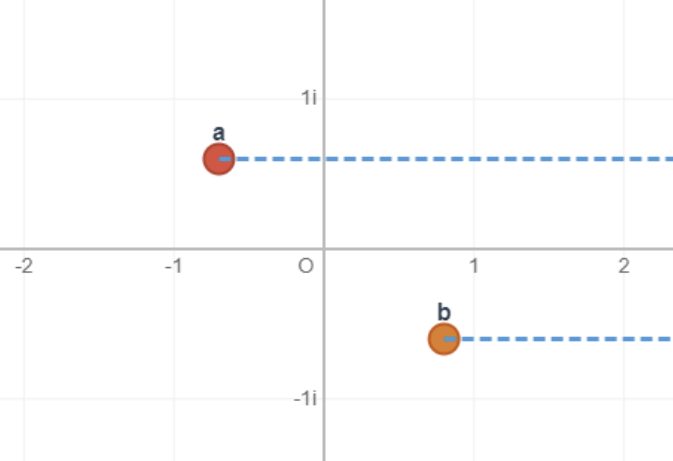
在上面的讨论中，考虑函数$w=\sqrt{z-a}$，自变量$z$绕点$a$旋转两圈（同时也是绕无穷远点$\infty$旋转）其函数值才能复原，因此我们可以说$z=a$和$z=\infty$是函数$w=\sqrt{z-a}$的分支点，其分支指数为2。

讨论函数：

\[ w = \sqrt[4]{(z-a)(z-b)} \]

我们写成辐角形式：

\[ \begin{aligned} w^4 &= r_1r_2e^{i(\theta_1+\theta_2)}\\ 4\arg w &= \theta_1 + \theta_2 \end{aligned} \]

可以看，当$z$绕$z=a$和$z=b$四圈才能让函数值复原，因此其分支指数为4；而同时绕两个点（$即绕z=\infty$）两次即可复原，分支指数为2。

要想让其为单值函数，必须做割线使得$z$不能绕任意一个分支点一圈，因此通常我们分别做连接$z=a$和$z=\infty$的射线和连接$z=b$和$z=\infty$的射线。

Reimann面¶

另一种方法是，规定复变函数在某一点的值，描述其沿某一路径运动到另一点的值。

先考虑函数$w = \sqrt{1-z}$，规定$w(2) = -i$，考虑$C_1$和$C_2$两种路径：

路径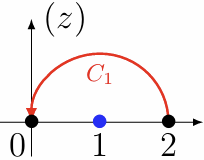
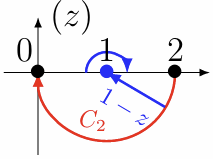$\Delta \arg(1-z)$	$\pi$	$-\pi$
$\arg(1-z)$	$(4k-1)\pi + \pi = 4k\pi$	$(4k-1)\pi - \pi = (4k-2)\pi$
$w$	$e^{\frac{4k\pi}{2}i} = 1$	$e^{\frac{(4k-2)\pi}{2}i} = -1$

在几何图形上，我们可以视作两个平面粘合起来（其实这个图形不能用三维描述）：

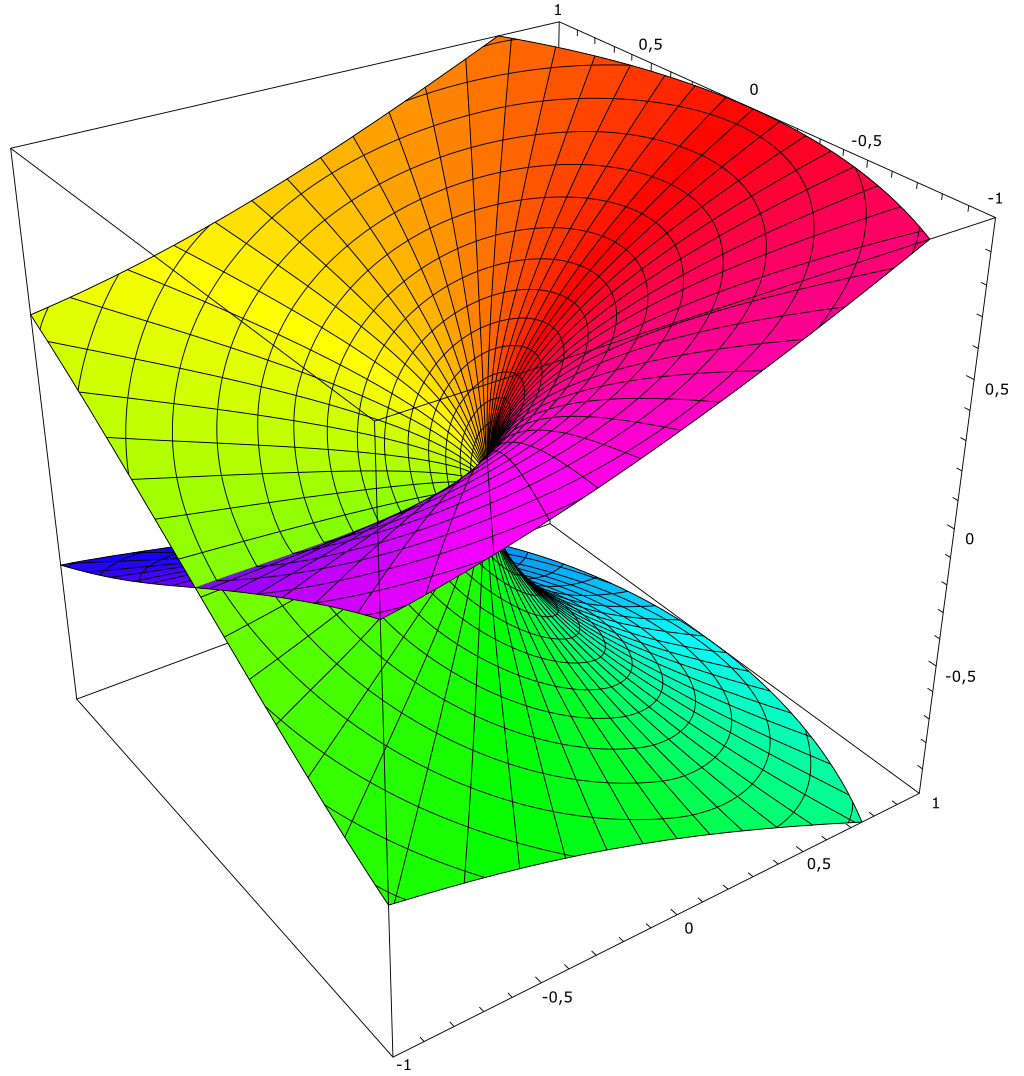
f（z） = z1/2

可以看到对于任意点绕原点的运动，只有在这个诡异的平面上转两圈才能复原；这种曲面就是Reiman面，对于这种根式函数有二叶Reiman面。

对数函数¶

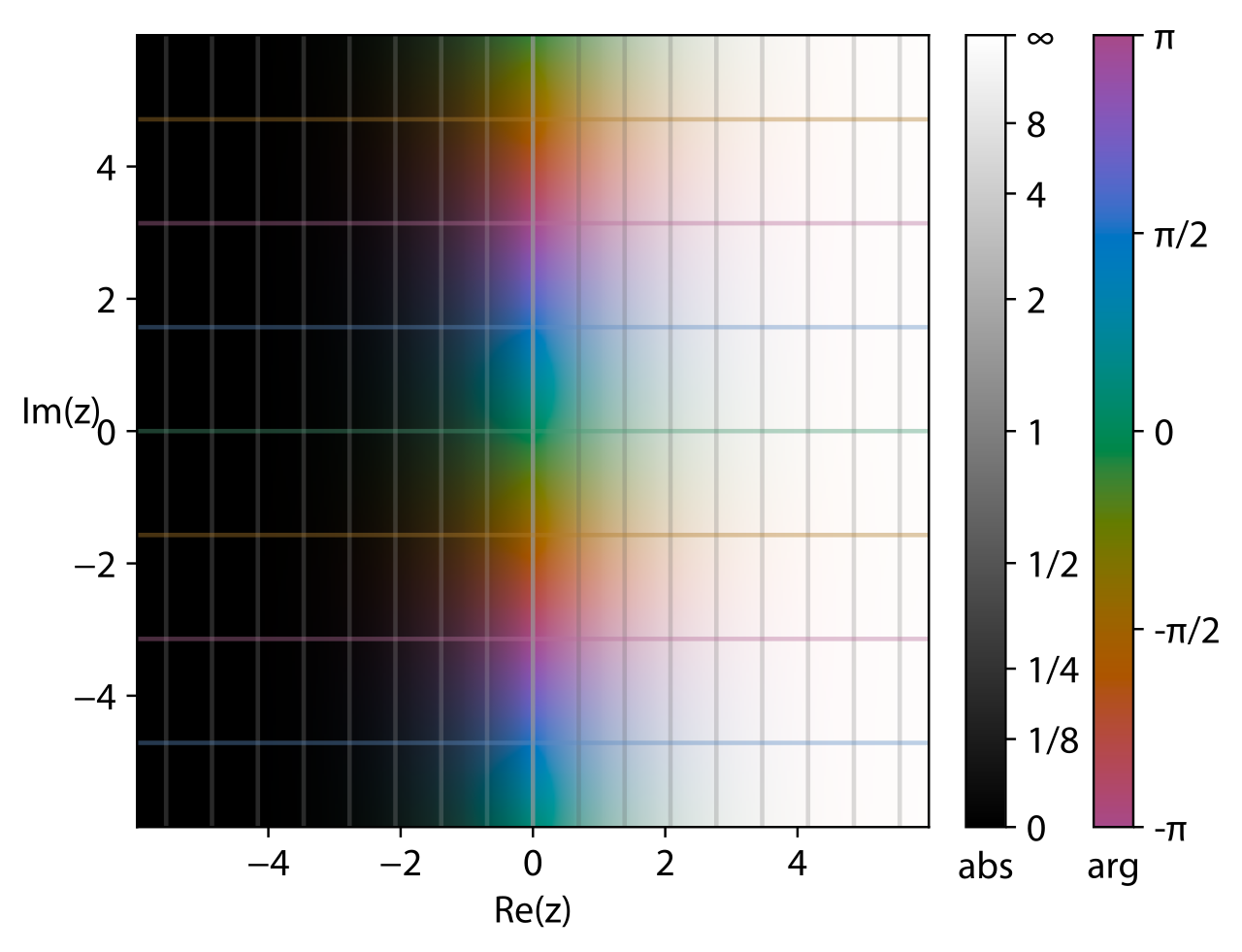
考虑复平面的对数函数： $$ w = \ln(z) $$ 令$w = u+iv$, $z = re^{i\theta}$，我们有： $$ \begin{gathered} u = \ln r = \ln \abs{z}, v= \theta + 2n\pi \ w = \ln \abs{z} + i(\arg{z} + 2n\pi) \end{gathered} $$ 也就是其每一个$z$空间内的点对应$w$空间实部相同的无数点：

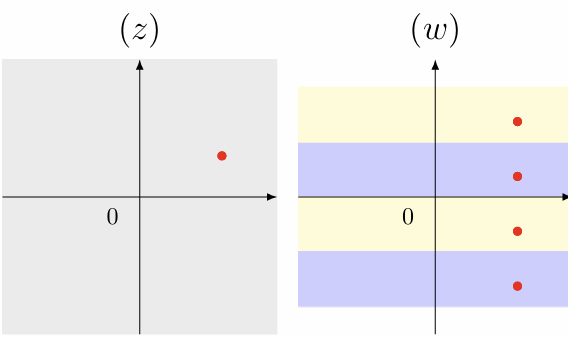
其限制在$[-\pi,\pi)$内的函数图像：

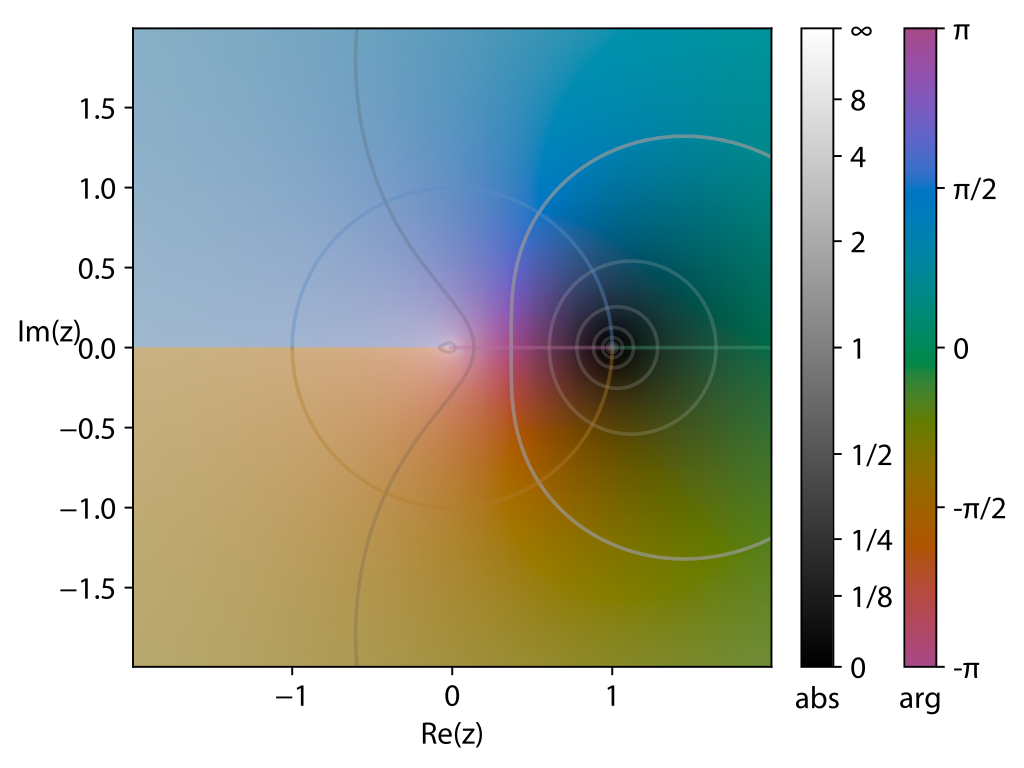
A density plot. In the middle there is a black point, at the negative axis the hue jumps sharply and evolves smoothly otherwise.

显而易见其分支点是$z=0$和$z=\infty$，于是做原点出发的射线可以使对数函数$\ln z$单值化。其Reiman面是无穷叶的：

logz

路径
\(\Delta \arg(1-z)\)	\(\pi\)	\(-\pi\)
\(\arg(1-z)\)	\((4k-1)\pi + \pi = 4k\pi\)	\((4k-1)\pi - \pi = (4k-2)\pi\)
\(w\)	\(e^{\frac{4k\pi}{2}i} = 1\)	\(e^{\frac{(4k-2)\pi}{2}i} = -1\)